ANSWER COMING SOON
How do dumb babies and blind puppies make money for deaf pussies with magic play money created with overlapping vertical dum sums of 99 digits?
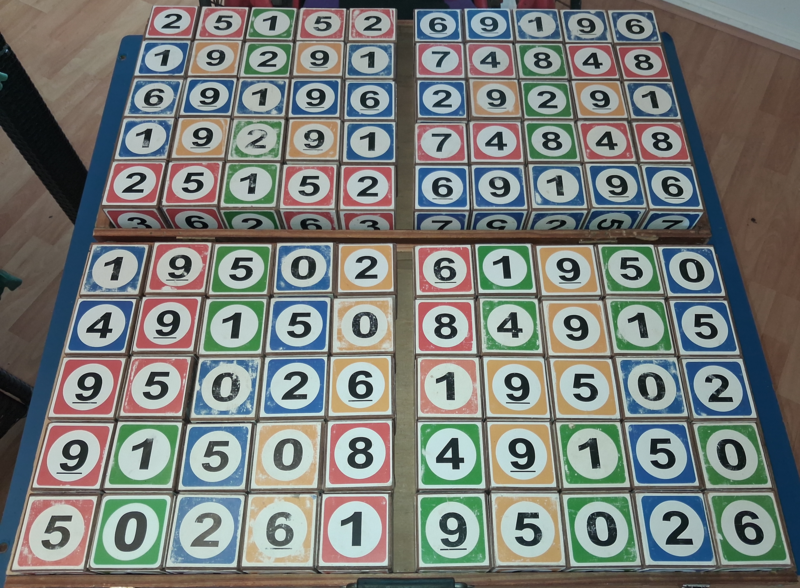
Notice 6+1=7 and 7+84=19 backwards
Notice 5+0=5 and 5+15=02 backwards
Notice 2+6=8 and 8+08=61 backwards
Which digit is missing under blue dot
Notice top left is horizontal and vertical rainbow relating to top left 9 square
digits relating to birthdate 25 dec 1961 with digital root of 9 in middle. Babies can choose any 9 digits which are then rainbowed with help.
www.bobcoin.com
FOR SALE
$99 .com domains about to expire
...more coming
Fair Dinkum! Mrs Noughtfear had the vision to take over the domain of a former Queensland Government and utilise it to make dummies rich with magic play money. She succeeded
in registering the trademark Big Bank of Australia in relation
to magic play money! She is giving away her secret ways
of baffling AI with her 100 digit dum sums which can be
jumbled and easily unjumbled! So who is going to be the first
to buy a $99 domain?
Notice pattern, same digit, same digit plus 1 and partners of 10
Notice 1 plus 3 is 4 and 4 plus 29 is 33
Notice 3 plus 0 plus 77 is 80
displayed backwards. What is next number after 808?
How do babies and dummies manipulate unknown numbers to create dum sums that add to backwards totals?
So jumblebaby.com fetched $99 we have to make it worth millions!
SUITABLE FOR BABIES